曲面生成帮
1.1- 软件大小:68.3MB
- 更新时间:2024-06-06
- 星级指数:
- 软件平台:电脑版
- 软件语言:简体中文
- 系统类型:支持32/64位
- 软件授权:免费
- 下载次数:18
- 安全监测:[无病毒, 正式版, 无插件]
- 操作系统:winall/win7/win10/win11
本地纯净下载纯净官方版
软件介绍
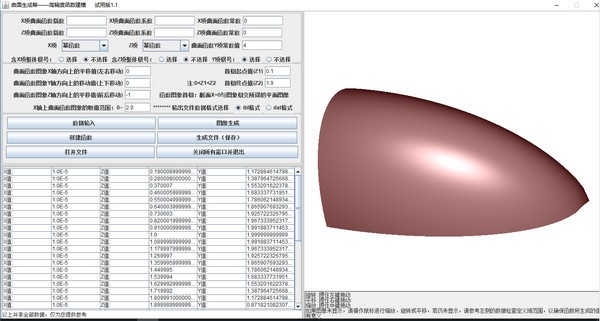
 曲面生成帮官方版是一款十分优秀且好用的曲面生成软件,曲面生成帮官方版主要用途为生成3D曲面模型,作为常用CAD软件的辅助软件而使用。用户根据需要完成函数输入,即可生成所需曲面。
曲面生成帮官方版是一款十分优秀且好用的曲面生成软件,曲面生成帮官方版主要用途为生成3D曲面模型,作为常用CAD软件的辅助软件而使用。用户根据需要完成函数输入,即可生成所需曲面。
基本简介
“曲面生成帮官方版”采用函数输入生成曲面的模式,仅需记住一些常用的曲面数学表达式或发挥自己的数学想象力就可生成,操作简便,所生成的曲面表达准确,并可将数据导入PROE或UG,方便用户进一步的开发使用。
软件使用步骤(完成3个模块的填写或选择):
(坐标系为右手系,X轴向右,Y轴向上,Z轴与观察方向相反,限定Z>0,X>0)
软件安装
软件日志
使用方法
软件图集
相关软件推荐
软件更新

芝麻时钟37.6MB|2024-11-06
直接下载
Chandler电脑版34MB|2024-11-06
直接下载
浩辰CAD看图王电脑版88.84MB|2024-11-06
直接下载
浩辰CAD看图王4.9MB|2024-11-06
直接下载
搜狗拼音输入法149.82MB|2024-11-06
直接下载
搜狗输入法149.82MB|2024-11-06
直接下载
搜狗拼音输入法电脑版149.82MB|2024-11-06
直接下载
搜狗拼音输入法Win版149.82MB|2024-11-06
直接下载
搜狗拼音输入法客户端149.82MB|2024-11-06
直接下载